4851. Детали
Предприятие “Авто-2012” выпускает
двигатели для известных во всём мире автомобилей. Двигатель состоит ровно из n
деталей, пронумерованных от 1 до n, при этом деталь с номером i
изготавливается за pi секунд. Специфика предприятия “Авто-2012” заключается
в том, что там одновременно может изготавливаться лишь одна деталь двигателя.
Для производства некоторых деталей необходимо иметь предварительно
изготовленный набор других деталей.
Генеральный директор “Авто-2012” поставил
перед предприятием амбициозную задачу – за наименьшее время изготовить деталь с
номером 1, чтобы представить её на выставке.
Требуется написать программу,
которая по заданным зависимостям порядка производства между деталями найдёт
наименьшее время, за которое можно произвести деталь с номером 1.
Вход. Первая строка содержит n (1 ≤ n ≤ 105) натуральных чисел p1, p2,
..., pn, определяющих
время изготовления каждой детали в секундах.
Каждая из следующих n
строк описывает характеристики производства деталей. Здесь i-ая строка содержит список деталей, которые требуются для
производства детали с номером i. В
списке нет повторяющихся номеров деталей. Список может быть в том числе пустым –
тогда ему будет соответствовать пустая строка! Сумма длин всех списков не
превосходит 200000.
Известно, что не существует циклических зависимостей в
производстве деталей.
Выход. Вывести
минимальное время (в секундах), необходимое для скорейшего производства детали
с номером 1.
|
Пример входа 1 |
Пример выхода 1 |
|
100
200 300 2 2 1 |
300 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
3 5 1 2 3 1 4 4 |
6 |
РЕШЕНИЕ
графы –
топологическая сортировка
Анализ алгоритма
Построим граф
зависимостей деталей и обернем граф. Для производства детали с номером 1
следует произвести все детали, достижимые из нее (первая деталь от всех их
зависит). Деталь i
изготавливается за pi секунд, припишем i-ой вершине
вес pi.
Запустим поиск в
глубину из вершины 1 и вычислим сумму весов всех достижимых из нее вершин
(включая ее саму). Это и будет искомое минимальное время.
Пример
Рассмотрим
первый пример. Построим граф зависимостей деталей (слева) и обратный ему граф
(справа).

Первая деталь
зависит от второй. Вторая деталь не зависит ни от какой другой. В обратном
графе из первой вершины существует путь только во вторую, следовательно общее
время, через которое можно произвести первую деталь, равно 100 + 200 = 300
(производим сначала вторую деталь, затем первую).
Рассмотрим
второй пример: граф и ему обратный.
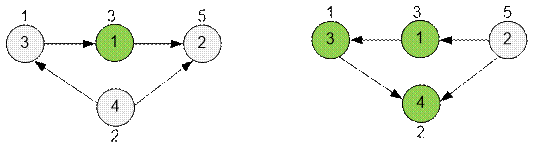
В обратном графе
путь из первой вершины существует в 3 и 4. Время, через которое можно
произвести первую деталь, равно 3 + 1 + 2 = 6.
Реализация алгоритма
Время
изготовления деталей храним в массиве p.
#define MAX 100010
long long p[MAX];
Объявим граф g и
массив used пройденных вершин для
поиска в глубину.
int
used[MAX];
vector<vector<int> > g;
Функция dfs реализует поиск в глубину. Для детали (вершины) v вычисляем наименьшее время, через
которое она может быть изготовлена. Оно равно непосредственному времени
изготовления детали p[v] плюс время
производства деталей, от которых зависит v.
Детали производятся одним агрегатом – то есть последовательно а не параллельно.
long long dfs(int v)
{
used[v] = 1;
long long res = p[v];
for (int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (!used[to]) res += dfs(to);
}
return res;
}
Основная часть программы. Количество деталей не известно,
читаем их до конца строки, их количество подсчитываем в переменной n. Время изготовления деталей заносим в
массив p.
n
= 1;
while(scanf("%lld%c",&p[n],&ch), ch != '\n') n++;
Читаем информауию о зависимостях между деталями в
производстве.
g.resize(n+1);
for(i
= 1; i <= n; i++)
{
gets(s);
stringstream in(s);
Для производства детали i следует изготовить все детали, номера которых находятся в строке s. По строке s строим поток in. Для
каждого числа a из потока строим
ребро i ® a.
while (in >> a)
g[i].push_back(a);
}
Вычисляем и выводим наименьшее время изготовления детали
номер 1.
memset(used,0,sizeof(used));
res
= dfs(1);
printf("%lld\n",res);